Ouin, PI ?

Comme à mes habitudes, à l’approche des fêtes, je vous ai préparé un petit article un peu différent que ceux que je fais d’habitude. L’idée m’est venue en regardant une vidéo de la chaîne Numberphile sur YouTube. La vidéo traitait d’un sujet connexe, mais ça m’a aidé à finalement comprendre ce que j’avais vu plus jeune dans le RPG Well of Souls. Ce jeu contenait un cheat qui permettait d’estimer PI en temps réel grâce à une simulation. C’est ce qu’on va essayer de recréer aujourd’hui !

Les sources de cet article sont disponibles ici.

Pourquoi estimer PI ?

En tant que programmeur, estimer PI avec la méthode que je vais vous présenter est non seulement très cool, mais aussi un beau petit défi. De plus, PI est un nombre qu’on retrouve partout, même à des endroits assez étranges, en plus d’être un nombre irrationnel. Je trouve personnellement très intéressant de voir qu’on arrive à calculer PI de plusieurs façons différentes et je crois que cette simulation est très agéable à développer et regarder.

Bref, parfait pour ne pas se casser la tête avant les fêtes! Amusons-nous 🙂

Comment fonctionne la simulation ?

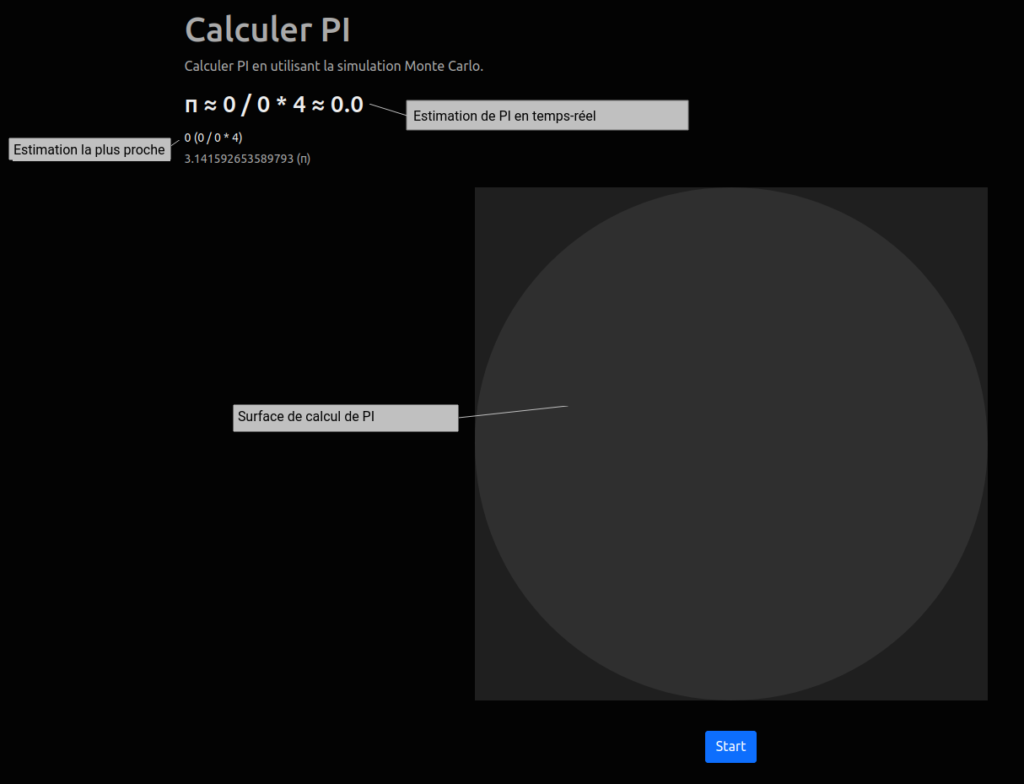
Imaginez-vous une cible pour un jeu de dart. Puis, tracer un carré de la même dimension de côtés que le diamètre de la cible, comme ceci :

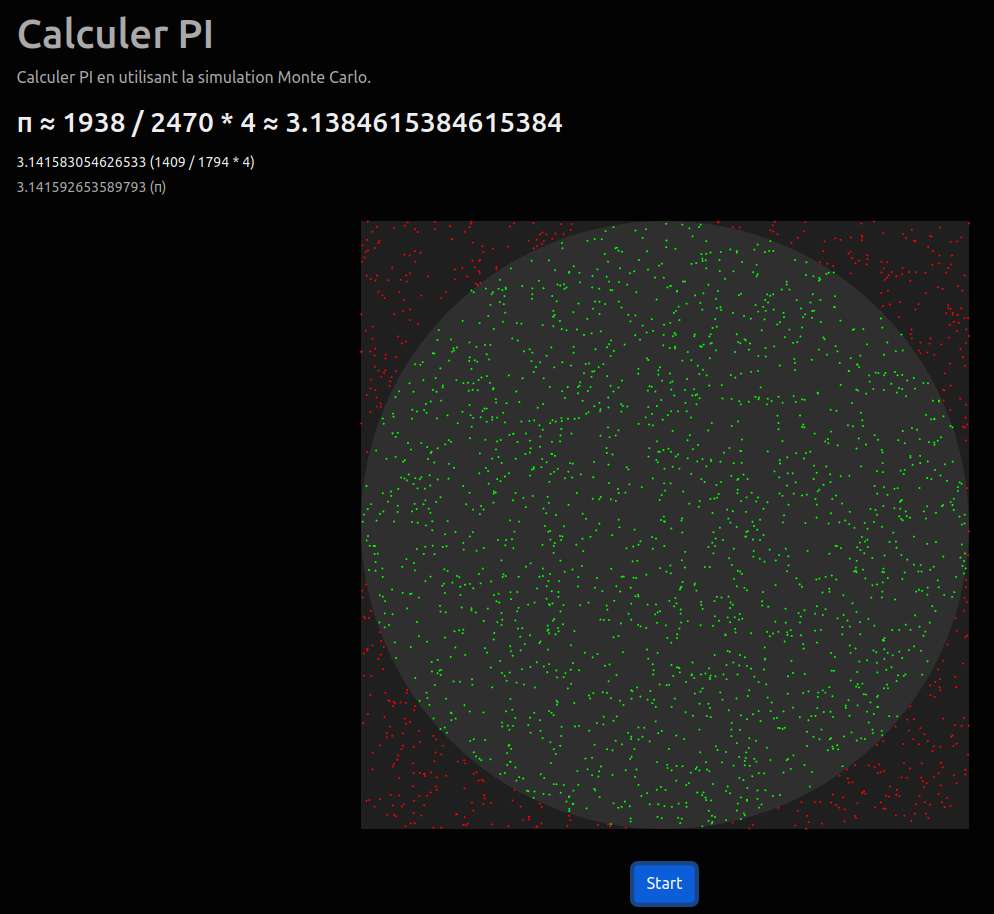
Maintenant, il faut lancer une infinité de darts vers cette cible. Notre approximation de PI sera le nombre de lancers sur la cible divisé par le nombre total de lancers multiplié par 4.

Cette simulation s’appelle la méthode de Monte-Carlo.

Le code

L’objectif ici étant de s’amuser, j’ai décidé de faire l’exercice avec HTML et JavaScript. Il y aura donc un canevas sur lequel on dessinera des points aléatoires. Je vais donc avoir besoin de :

Une vue, en HTML
Un modèle de vue, pour me permettre d’afficher de l’information dans la vue
Un moteur pour gérer l’animation
Un calculateur pour estimer PI avec la méthode Monte-Carlo
Un dépôt pour stocker l’estimation qu’on aura trouvé qui sera la plus près de PI
Une classe d’application pour orchestrer tout ça

La vue

Pour la vue, nous avons besoin de quelques pour injecter les valeurs calculées par le calculateur, d’un <canevas> pour dessiner la cible et les points et d’un bouton pour lancer le tout. Avec l’aide de Bootstrap, ça ressemble à ceci :

Voir le code complet de la vue.

Le modèle de vue

Cette classe a la responsabilité d’abstraire le code HTML de la vue. Elle doit donc exposer des mutateurs qui auront la responsabilité d’aller injecter la nouvelle valeur dans les . En procédant de cette façon, tout le reste du code JavaScript ignorera qu’il y a une page HTML. Créons la classe :

class ViewModel {
  // code
}

class ViewModel {

// code

}

Afin d’y aller au plus simple possible, cette classe garde une copie en attributs des éléments HTML suivants :

piElement = l’instance du HTMLElement représentant le qui affiche la valeur approximative de PI
dotsInCircleElement = l’instance du HTMLElement représentant le qui affiche le nombre de points générés à l’intérieur du cercle
totalDotsElement = l’instance du HTMLElement représentant le qui affiche le nombre total de points générés
startButtonElement = l’instance du HTMLElement représentant le bouton pour lancer la simulation
closestEstimationElement = l’instance du HTMLElement représentant le qui affiche le record d’approximation de PI (persité)
dotsInCircleClosestEstimationElement = l’instance du HTMLElement représentant le qui affiche le nombre de points générés à l’intérieur du cercle en lien avec le record persisté
totalDotsClosestEstimationElement = l’instance du HTMLElement représentant le qui affiche le nombre total de points générés en lien avec le record persisté
piRealValueElement = l’instance du HTMLElement représentant le qui affiche la valeur de Math.PI
onclickStartButton = une méthode qui sera appelée lors du clic sur le bouton Start

Puis, dans le constructeur, on récuère ces instances avec getElementById(), en prennant soin de sortir les ID d’éléments dans un fichier de constantes :

this.piElement = document.getElementById(PI_ELEMENT_ID);

1	this.piElement = document.getElementById(PI_ELEMENT_ID);

Ensuite, on expose des mutateurs pour chacun des éléments html, comme ceci :

setPi(pi) {
  this.piElement.innerHTML = pi;
}

setPi(pi) {

this.piElement.innerHTML = pi;

}

Finalement, il reste à attacher la fonction onclickStartButton au véritable bouton dans le DOM à l’aide d’une méthode comme celle-ci :

_bindEvents() {
  this.startButtonElement.addEventListener("click", () =>
    this.onclickStartButton()
  );
}

_bindEvents() {

this.startButtonElement.addEventListener("click", () =>

this.onclickStartButton()

);

}

Voir le code complet du modèle de vue.

Le moteur

Le moteur ici a la responsabilité de s’attacher au cycle de dessin du navigateur pour faire une animation fluide. Il exposera des méthodes pour dessiner sur le canevas ainsi une méthode qui sera appelée à chaque cycle de dessin. Créons la classe :

class Engine {
}

1 2	class Engine { }

Le moteur va devoir garder une copie de l’instance de HTMLElement qui représente le <canevas> ainsi que son contexte 2D. Il doit aussi exposer les méthodes de dessin, comme pour dessiner un point d’une certaine couleur sur le canevas :

drawDot(x, y, color) {
  this.ctx.beginPath();
  this.ctx.arc(x, y, 1, 0, 2 * Math.PI, false);
  this.ctx.fillStyle = color;
  this.ctx.fill();
}

drawDot(x, y, color) {

this.ctx.beginPath();

this.ctx.arc(x, y, 1, 0, 2 * Math.PI, false);

this.ctx.fillStyle = color;

this.ctx.fill();

}

On termine par une méthode pour lancer l’animation, puis la boucle d’animation en elle-même :

start() {
  this._loop();
}

_loop() {
  this.onloop();
  requestAnimationFrame(this._loop.bind(this));  
}

start() {

this._loop();

}

_loop() {

this.onloop();

requestAnimationFrame(this._loop.bind(this));

}

Ici, onloop est une fonction qui sera appelée à chaque cycle.

Voir le code complet du moteur.

Le calculateur Monte-Carlo

Cette classe servira à encapsuler l’algorithme de calcul pour la simulation. Comme expliqué plus haut, on doit générer des points aléatoires. Cette classe sera donc responsable de faire ces calculs et de garder l’estimation la proche de la valeur de Math.PI.

class MonteCarloPiComputer {
  dotsInCircle = 0;
  totalNumDot = 0;
  closestEstimation = {
    distance: Infinity,
    value: 0,
    dotsInCircle: 0,
    totalNumDot: 0,
  };

  constructor(centerX, centerY, radius) {
    this.centerX = centerX;
    this.centerY = centerY;
    this.radius = radius;
  }
}

class MonteCarloPiComputer {

dotsInCircle = 0;

totalNumDot = 0;

closestEstimation = {

distance: Infinity,

value: 0,

dotsInCircle: 0,

totalNumDot: 0,

};

constructor(centerX, centerY, radius) {

this.centerX = centerX;

this.centerY = centerY;

this.radius = radius;

}

Puis, on expose la méthode qui nous permet de générer un point aléatoire, tout en comptabilisant l’information :

nextDot() {
  const x = Math.random() * this.radius * 2 + this.centerX - this.radius;
  const y = Math.random() * this.radius * 2 + this.centerY - this.radius;
  const inCircle = this._isDotInCircle(x, y);

  if (inCircle) {
    this.dotsInCircle++;
  }

  this.totalNumDot++;
  this._setRecordIfClosest();

  return { x, y, inCircle };
}

nextDot() {

const x = Math.random() * this.radius * 2 + this.centerX - this.radius;

const y = Math.random() * this.radius * 2 + this.centerY - this.radius;

const inCircle = this._isDotInCircle(x, y);

if (inCircle) {

this.dotsInCircle++;

}

this.totalNumDot++;

this._setRecordIfClosest();

return { x, y, inCircle };

}

Afin de déterminer si le point est dans le cercle, nous n’avons qu’à mesurer la distance qui le sépare du centre du cercle et de le comparer avec son rayon.

_isDotInCircle(x, y) {
  const distance = Math.sqrt(
    Math.pow(x - this.centerX, 2) + Math.pow(y - this.centerY, 2)
  );
  return distance <= this.radius;
}

_isDotInCircle(x, y) {

const distance = Math.sqrt(

Math.pow(x - this.centerX, 2) + Math.pow(y - this.centerY, 2)

);

return distance <= this.radius;

}

Puis on expose la méthode permettant de faire l’estimation de PI :

approximatePI() {
  return this.dotsInCircle / this.totalNumDot * 4.0;
}

approximatePI() {

return this.dotsInCircle / this.totalNumDot * 4.0;

}

Voir le code complet du calculateur.

Le dépôt pour stocker le record

Étant donné que PI va se calculer de plus en plus précisément à mesure qu’on génère des points, il me paraissait intéressant de pouvoir stocker l’estimation de PI qui est la plus près de Math.PI. Le dépôt a donc la responsabilité de stocker l’information dans le localStorage du navigateur.

class PiEstimationRepository {
  findClosestEstimation() {
    const bestPiEstimationRaw = localStorage.getItem('closestPiEstimation');
    if (bestPiEstimationRaw) {
      return JSON.parse(bestPiEstimationRaw);
    } else {
      return {
        value: 0,
        dotsInCircle: 0,
        totalNumDot: 0,
        distance: Infinity,
      };
    } 
  }

  saveClosestEstimation(piEstimation) {
    localStorage.setItem('closestPiEstimation', JSON.stringify(piEstimation));
  }
}

class PiEstimationRepository {

findClosestEstimation() {

const bestPiEstimationRaw = localStorage.getItem('closestPiEstimation');

if (bestPiEstimationRaw) {

return JSON.parse(bestPiEstimationRaw);

} else {

return {

value: 0,

dotsInCircle: 0,

totalNumDot: 0,

distance: Infinity,

};

}

saveClosestEstimation(piEstimation) {

localStorage.setItem('closestPiEstimation', JSON.stringify(piEstimation));

}

Voir le code complet du dépôt.

La classe applicative

Cette classe fait office d’orchestrateur pour les autres classes. Elle permet de créer les instances nécessaires, de générer la cible sur laquelle on dessine les points ainsi que d’exécuter la boucle principale via la méthode onloop() du moteur :

onloop() {
  const dot = this.piComputer.nextDot();
  const color = dot.inCircle ? DOT_INSIDE_CIRCLE_COLOR : DOT_OUTSIDE_CIRCLE_COLOR;
  
  this.engine.drawDot(dot.x, dot.y, color);
  this._persistClosestEstimationIfNecessary();
  this._displayPiComputerValues();
}

onloop() {

const dot = this.piComputer.nextDot();

const color = dot.inCircle ? DOT_INSIDE_CIRCLE_COLOR : DOT_OUTSIDE_CIRCLE_COLOR;

this.engine.drawDot(dot.x, dot.y, color);

this._persistClosestEstimationIfNecessary();

this._displayPiComputerValues();

}

Voir le code complet de la classe applicative.

Pour exécuter l’application

Prérequis

npm install -g http-server
git clone https://gitlab.com/blogue-ezo/simulation-monte-carlo

1 2	npm install -g http-server git clone https://gitlab.com/blogue-ezo/simulation-monte-carlo

Pour lancer :

npm install
http-server

1 2	npm install http-server

Puis ouvrir le navigateur à l’adresse indiquée dans la console.

Conclusion

Aujourd’hui, on a laissé de côté les trucs compliqués pour avoir du plasir avec du code. Personnellement, ce genre d’exercice me permet de décrocher du code que j’ai à produire pour mon client. Ça permet d’exercer son côté créatif en utilisant un algorithme amusant.

Si vous avez apprécié, n’hésitez pas à partager avec vos collègues et amis 🙂 @+

Partager sur Facebook

Partager sur Twitter

Ouin, PI ?

Pourquoi estimer PI ?

Comment fonctionne la simulation ?

Le code

La vue

Le modèle de vue

Le moteur

Le calculateur Monte-Carlo

Le dépôt pour stocker le record

La classe applicative

Pour exécuter l’application

Conclusion

60

SHARES

Écrit par

Sylvain Cloutier

Tags

Commentaires

Laisser un commentaire

Annuler la réponse.

Catégories

Suivez-nous par courriel!

Publications récentes

Ce qu’on dit sur Twitter

Ouin, PI ?

Pourquoi estimer PI ?

Comment fonctionne la simulation ?

Le code

La vue

Le modèle de vue

Le moteur

Le calculateur Monte-Carlo

Le dépôt pour stocker le record

La classe applicative

Pour exécuter l’application

Conclusion

60

SHARES

Articles qui pourraient vous intéresser :

Écrit par

Sylvain Cloutier

Tags

Commentaires

Laisser un commentaire

Annuler la réponse.

Catégories

Suivez-nous par courriel!

Publications récentes

Ce qu’on dit sur Twitter

Suivez-nous!